諺
递归相关的形而上思考整理
2022-02-28 / modified at 2024-02-15 / 2.6k words / 9 mins

本文整理了递归的历史和观点，并综述了各个时期的学者对递归的哲学思考。

递归是形而上的存在问题（研究分类事物的视角/范式/数量级），首先要先定义好时间观与存在观。不要用基于古典逻辑或延展的视角去“拆解”递归中的思路，甚至你掌握的形式工具越多，理解难度反而更大。

本文从开始思考到找到参考书，搁置接近两年，是当前难度最高的非IT技术写作了。无论是查资料，还是下定义，感觉对研究对象都充满了无力感，因此本文非专业论文，仅仅是非专业的随想。

阅读方法论

  • 尽可能从历史的角度，综述各个学科的观点
  • 反复二次阅读

递归的历史

主要历史事件

尽可能按照时间排序

强调用符号体系去认识世界的时代：

  • 莱布尼茨（1646～1716）：全才。发明了微积分。设想通过形式化符号，即“普遍文字”（universalcharacteristic）作为符号来描述思考，当前他只是提出了初代的理论。同时基于八卦图验证必提出了二进制。他的《单子论》是跨时代的，但是过于还原主义/理性主义，对“关系”的表达也较弱。
  • 乔治·布尔：将古典逻辑转为数学形式，当前编程中的Boolean值就是以他为命名的。
  • 弗雷格：他的《概念文字》是现代逻辑学的开山之作，可以精准地形式化描述，当前高中的数学逻辑基础课和这里基本上相同了，比如“且/或”等
  • 罗素（1872～1970）：英国哲学家、数学家和逻辑学家，创立了分析哲学，提出了摹状词理论。

递归产生

  • 大卫·希尔伯特 Hilbert（1862～1943）：第一次提出了递归。提了一堆问题的人。

  • 库尔特·哥德尔（1906～1978）：1931，在证明“不完备”猜想中，他引入递归，并自创了类编程语言，主要关注“反思逻辑”。

  • 阿隆佐·邱奇：1936年发表可计算函数的第一份精确定义（λ演算），他是图灵的老师

  • 图灵：图灵奖的图灵。这位被王垠喷惨了，比较尴尬，因为理论上λ演算已经是最优雅的，而落地工程又是冯诺依曼做的。

  • 冯诺依曼：第一天真正能用起来的通用计算机。

  • 维纳：控制论

  • 戴克斯特拉（dijkstra）：结构化编程-递归程序，递归函数在1960年被引入

  • 近现代：逻辑式语言，比如Prolog或者miniKanren

关于西方哲学的主要事件，可以参考另一篇文章。

机械与有机的认知

机械论(Mechanism)：笛卡尔的线性因果认知

常见的认知是基于目的（比如目的因）或者过程的认知方法。这是一种还原主义，它一般隐含了因果、覆盖等线形思维（语言）来进行延展认知，通过直觉就可以感受。常见的两种

  • 结构逻辑：无时间概念与推导过程，比如加减法，组合计算等
  • 古典数学逻辑：推到过程涉及到时间概念，比如因为···所以···，如果···，三段论等高中课程

就算中间的步骤再多，只要“解剖分析”进行Top-down递推分解，这个事情就能解决。这些相关思考可以参考笛卡尔的《谈谈方法》或者机械论中的观点，也是工作中常见的西方的framework（比如WBS/PERT/MECE等方法论）。其实能达到这类工作能力已经很不错了。

机器有机论（mechano-organicism）

非线性思考：这里的“非线性”并不是指曲线思考，而是一种时刻自我调整的反馈过程[1]。它与线性因果相比，加入了反馈（feedback）机制，操作命令的用户信息（甚至包含观测）也是算法的一部分。这里是由维纳最先发表，即控制论。可以参考《人有人的用处》

其他类似翻译参考

  • 综合的：Synthetic
  • 计算的：Computational
  • 反身的：Reflexive
  • 衍生的：Derivative，比如PBKDF2算法，金融中的期货期权，AI里的收敛算法
  • 积累的：Accumulation，体现了时间性。
  • 熟成的：Aged，比如牛排/火腿/酒/咖啡，气味分子在特定的初始保存条件下经过时间的酝酿，最终形成特定的风味

递归的定义

定义

  • 在数学领域，属于离散数学集合论的归纳定义，这个定义对普通人而言在于门槛太高，要先掌握数学符号。
  • 在计算理论领域，最早由数学家哥德尔在“不完全定理”中提出，被称作“原始递归函数”，它与computability是等价的。定义为不断调用自己直至停机状态（预先规定、可执行的目标）的函数，递归函数一定是可计算的。可计算也一定是递归的。
  • 在哲学领域，被分类为有机体论/反馈 ，可以参考定义“循環因果關係的反身性（reflexive）運動”
  • 数字芯片的定义：时序逻辑，需要考虑引入寄存器来缓存结果，比如这篇博文就介绍了定义。

值得注意的是，“计算理论”和“计算机”是不同的概念，第一个本质是数学问题，里面是没有“内存/状态/寄存器”的实物或时间概念的，通用但是过于抽象。而计算机的本质就是“计算+寄存器”，虽然不优雅但是够用。

例子

比如Fibonacci sequence，用Java定义如下

1
2
3
4
5
6
7
// 本问题同时也是爬楼梯的问题
int fibonacci(int x){
  if(x<=1){
    return x;
  }
  return fibonacci(x-1) + fibonacci(x-2); 
}

目前课本只能用经验手段，从fib(0),fib(1)···延展举例来模拟其定义，但是大脑把这个例子背诵后，甚至把树的遍历背诵后，可以刷LeetCode题了，就真的“掌握”了递归吗？课本中的消除栈溢出，如何用dp来缓存结果，这两个工程手段很重要吗？（在groovy等语言中，都有开箱方案）

公式等号的歧义

以下公式，个人认为等号含义是不同的。第一个逻辑运算是不含时间特性的，它只是一个加法器

1
2
// 主谓的定义，无时间特性
2 = 1 + 1

而第二个等号是对一个本体下定义，它表示“时序关系”作用的结果，存在“寄存器”的时间概念，不等于执行了2次的发条。个人对fib(2)的理解是“f(0)随着时间发酵(递归函数)的特殊风味”。

1
2
// 存在的定义，有综合时间的特性
fib(2) = fib(1) + fib(0)

即使递归函数fib(k)的k在数字的角度上为离散的int类型，它在认识的解释中仍然是连续的，是衡量变化的尺度。不能用fib(k)的运动轨迹来代替fib本身。

为什么有人刷题“理解”递归更快？

刷题记忆不等于掌握了问题。这并不是一个理解力或者智力的问题，而是信念强度的问题。比如爬楼梯，很多人通过归纳猜想到了递归公式就直接用了。而我是“怀疑论”者，除非从数学有证明猜想，甚至在计算时始终都会去想反例去自己推翻自己。所以刷题上优势全无。

刷题和真实工程的设计是对立的，它在为你带来QuickWin的同时，也让你失去了好奇心、主动探索的机会（比如本文的思考）。

recursive与iteratively

iteratively是典型的机械式发条思考，可以用草稿中的1,2,3的绘制来代表时间的均质延伸，比如这样画框框来思考for循环中的时刻，比如two pointers等算法。

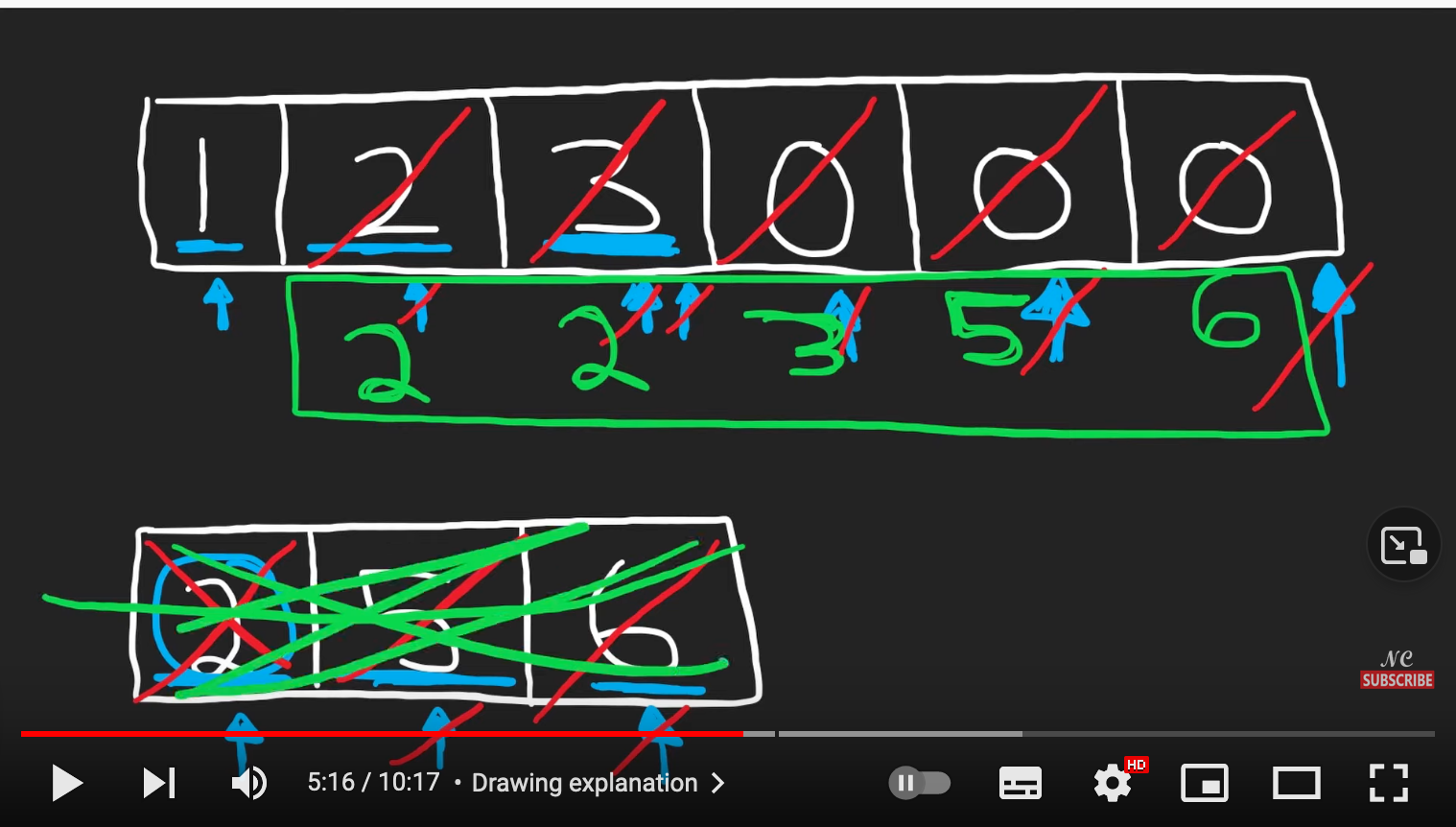
merge-sorted-array-in-place

From merge-sorted-array

相对于均质的iteratively思考， recursive 的思考是没有均质延伸的概念，而且是难以用图像来说明的，比如

  • 综合后的状态：比如回溯法backtrack
  • 产生的后果：比如编辑距离的长度，爬楼梯方法总数等，而不是某个具体的路径实例

递归的工程优化

一般来说,不推荐一步到位到工程级,常见工程优化两种

  • Top-down的memorization优化,即加一个map作为缓存
  • Buttom-up的迭代,即dp的for循环求积分

递归与状态机

递归中一定有状态机，可以为停机、回溯等操作，而且一定是可枚举的。

彩蛋：dijkstra戴克斯特拉

这位荷兰计算机专家有如下贡献，我们可以从他的背景/文章中更好地学习递归

  • mergesort
  • Dijkstra算法（迷宫）
  • PV信号量（与哲学家就餐问题）

更多可以看这里：https://www.dijkstrascry.com/

递归的扩展

  • 元胞自动机 cellular automata等仿真计算，复杂系统；所有的机器学习都是递归式的；所有机械在尽可能成为有机的机器
  • 控制论

冯·诺依曼的运动学模型与自动复制机

这种自动复制的机器人当前并未实现，但是在赛博朋克类型作品中大量存在，比如《Blame!》里的超構造体（Mega Structure），《Ghost In The Shell》的Ghost Dummy Machine 等。

递归为什么难

  • 理解层次：递归在于要用后天经验对象的运动轨迹去理解时间表象，进而分析纯粹理性的问题。
  • 语言与符号：需要将自然语言改写为摹状函数。

Reference

  1. 《递归与偶然》-P155 ↩